The pursuit of understanding bosonic excitations in the realm of quantum mechanics has led researchers from notable institutions—including the Freie Universität Berlin, University of Maryland, Google AI, and NIST—in their quest for precisely estimating Hamiltonian parameters. These collaborative efforts underscore the pivotal role of quantum simulations, which promise to stretch the bounds of classical computational capabilities. The work, which has recently surfaced in a pre-publication format on arXiv, indicates a significant leap in the methodologies utilized for navigating the complex landscape of quantum states and Hamiltonian parameters.
The Genesis of a Collaborative Effort
The journey of this enlightening research began during a conference in Brazil when Jens Eisert, the first author of the paper, received an unexpected call from colleagues at Google AI. They were grappling with challenges while calibrating their superconducting quantum chip—Sycamore—using Hamiltonian learning methods. Initially convinced that resolving the issues posed would be straightforward, Eisert soon recognized the complexity hidden beneath the surface. The intricacies involved in recovering Hamiltonian frequencies from their experimental data proved to be more formidable than anticipated.
Understanding this convoluted challenge demanded more than just intellectual acumen; it required the collaboration of skilled colleagues. With the help of Ph.D. students Ingo Roth and Dominik Hangleiter, the team ventured into uncharted territory, striving to develop a solid framework to tackle the problem using superresolution techniques. However, practical implementation led to further complexities, prolonging the research period significantly. Collaboration persisted, even with changing personnel; the commitment of the research team, including Jonas Fuksa and experimental lead Pedram Roushan from Google AI, remained steadfast despite initial frustrations.
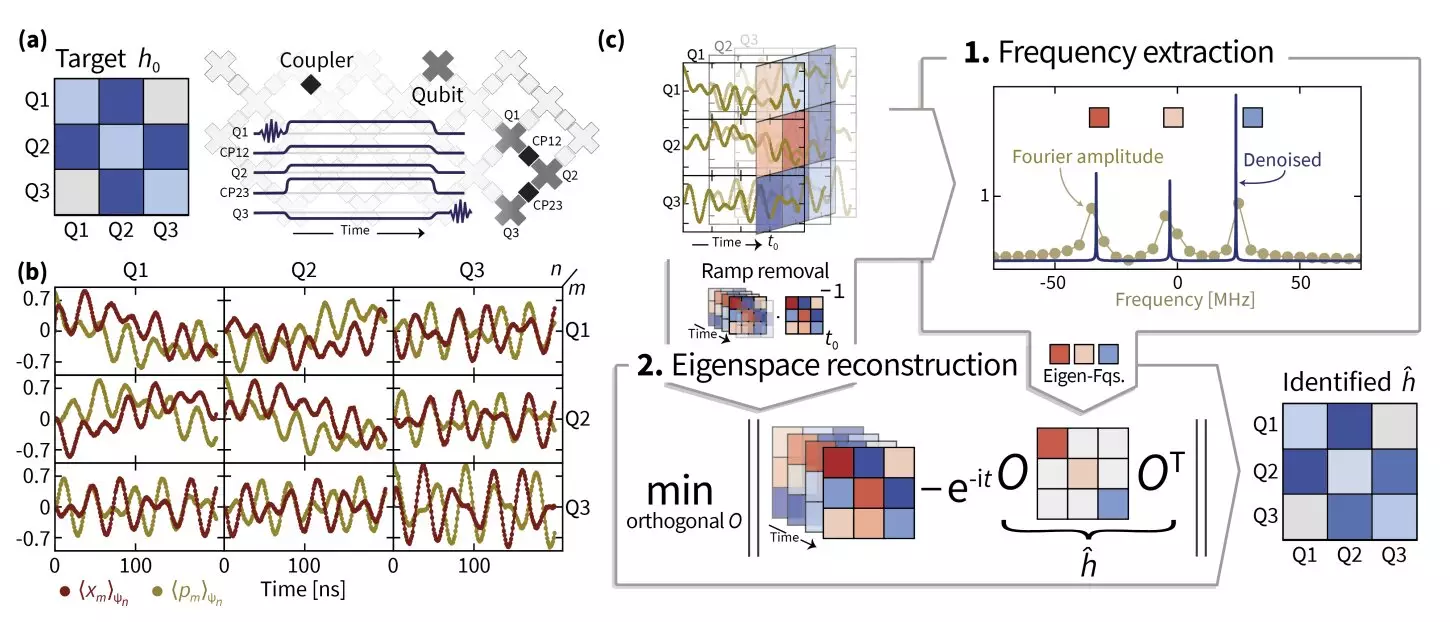
Central to the research was the implementation of advanced techniques aimed at understanding the Hamiltonian dynamics of a superconducting quantum simulator. The application of superresolution—specifically tailored to enhance eigenvalue estimation—was crucial in accurately determining the Hamiltonian frequencies. Manifold optimization followed as a key strategy for recovering eigenspaces of the Hamiltonian operator, involving sophisticated optimization algorithms designed to handle challenges presented by curved mathematical landscapes.
Eisert explains that the intricacies of the processes involved in switching Hamiltonian interactions on and off further complicated their task. The dynamics of these processes—as non-instantaneous and imperfect—had to be meticulously factored into their estimations. Their developmental journey culminated in TensorEsprit, a novel signal processing method that enabled the research team to robustly recover Hamiltonian details, overcoming challenges posed by large system sizes.
The research established a rigorous framework allowing for the robust identification of Hamiltonian parameters across a network of coupled superconducting qubits from two Sycamore processors—delivering promising results that hint at feasibility for scaling applications. The findings point to the significant potential of Hamiltonian learning methods in practical data applications, an area that has historically lagged in empirical research due to inherent methodological difficulties.
Eisert emphasizes the importance of accurately discerning eigenvalues to meaningfully recover eigenspaces, highlighting a crucial takeaway from their extensive endeavor. This complex road traveled underscored the challenges experienced by researchers attempting Hamiltonian learning, shedding light on the reasons for the scant literature surrounding the topic to date.
The research team’s future prospects are equally exciting, as they plan to extend their methodologies to broader interacting quantum systems. Another exciting avenue involves applying ideas derived from tensor networks to cold atom quantum systems, building on foundational work pioneered by physicist Immanuel Bloch. Eisert expresses optimism about the future significance of this field, emphasizing that the fundamental questions surrounding Hamiltonians remain crucial yet often overlooked—even at the introductory levels of quantum mechanics education.
Finally, as research delves deeper into the fabric of quantum mechanics, the potential implications for developing quantum technologies are undeniable. The groundwork laid through this collaboration could facilitate a deeper understanding of analog quantum simulators, ultimately paving the way toward high-precision quantum simulations. Eisert succinctly captures the transformative potential of these studies: “Analog quantum simulation allows complex quantum systems and materials to be researched in a new way, by recreating them under extremely precise conditions in the laboratory.”
This interdisciplinary effort culminates not only in technical advancements but in crystallizing the conceptual framework necessary for the next generation of quantum technologies.